从零开始的力扣刷题

刷题

回文数

📖 文字题解
方法一：反转一半数字
思路
映入脑海的第一个想法是将数字转换为字符串，并检查字符串是否为回文。但是，这需要额外的非常量空间来创建问题描述中所不允许的字符串。
第二个想法是将数字本身反转，然后将反转后的数字与原始数字进行比较，如果它们是相同的，那么这个数字就是回文。
但是，如果反转后的数

---

回文数

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。

回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

例如，121 是回文，而 123 不是。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/palindrome-number

方法一：反转一半数字

思路

映入脑海的第一个想法是将数字转换为字符串，并检查字符串是否为回文。但是，这需要额外的非常量空间来创建问题描述中所不允许的字符串。

第二个想法是将数字本身反转，然后将反转后的数字与原始数字进行比较，如果它们是相同的，那么这个数字就是回文。
但是，如果反转后的数字大于 int.MAX，我们将遇到整数溢出问题。

按照第二个想法，为了避免数字反转可能导致的溢出问题，为什么不考虑只反转 int数字的一半？毕竟，如果该数字是回文，其后半部分反转后应该与原始数字的前半部分相同。

例如，输入 1221，我们可以将数字 “1221” 的后半部分从 “21” 反转为 “12”，并将其与前半部分 “12” 进行比较，因为二者相同，我们得知数字 1221 是回文。

算法

首先，我们应该处理一些临界情况。所有负数都不可能是回文，例如：-123 不是回文，因为 - 不等于 3。所以我们可以对所有负数返回 false。除了 0 以外，所有个位是 0 的数字不可能是回文，因为最高位不等于 0。所以我们可以对所有大于 0 且个位是 0 的数字返回 false。

现在，让我们来考虑如何反转后半部分的数字。

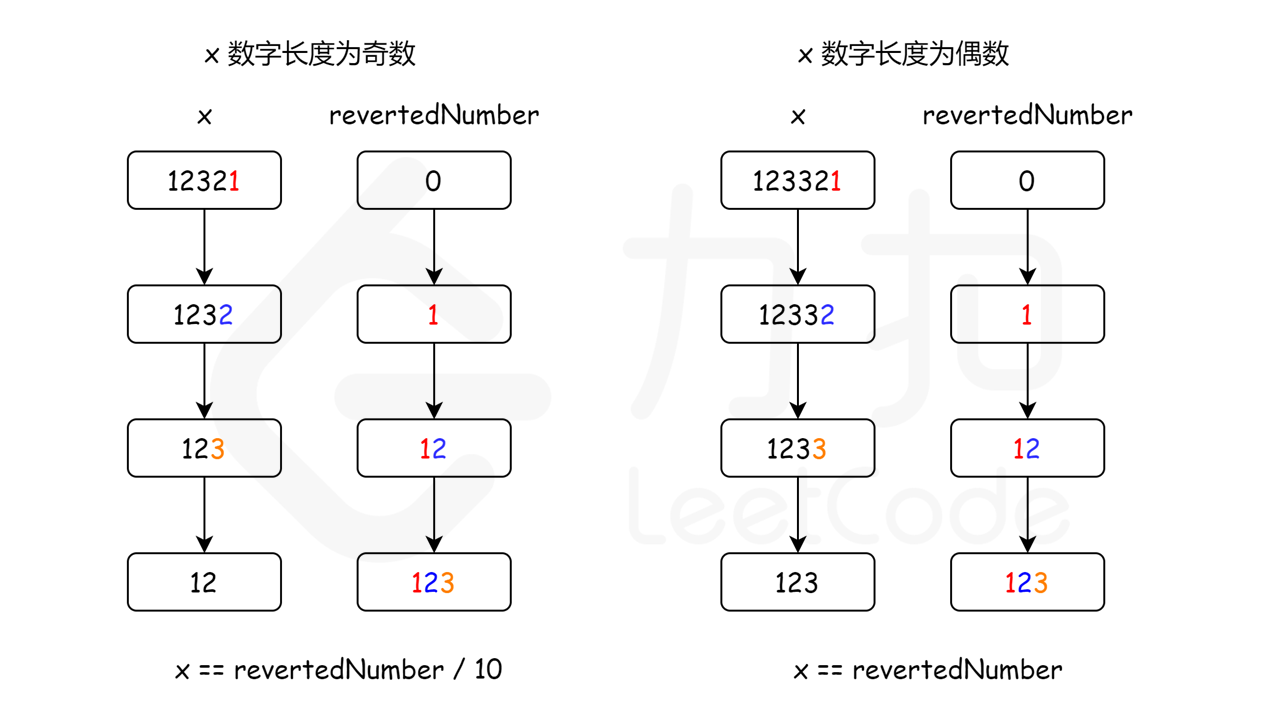
对于数字 1221，如果执行 1221 % 10，我们将得到最后一位数字 1，要得到倒数第二位数字，我们可以先通过除以 10 把最后一位数字从 1221 中移除，1221 / 10 = 122，再求出上一步结果除以 10 的余数，122 % 10 = 2，就可以得到倒数第二位数字。如果我们把最后一位数字乘以 10，再加上倒数第二位数字，1 * 10 + 2 = 12，就得到了我们想要的反转后的数字。如果继续这个过程，我们将得到更多位数的反转数字。

现在的问题是，我们如何知道反转数字的位数已经达到原始数字位数的一半？

由于整个过程我们不断将原始数字除以 10，然后给反转后的数字乘上 10，所以，当原始数字小于或等于反转后的数字时，就意味着我们已经处理了一半位数的数字了。

• C++
• C#
• Java
• TypeScript
• Golang

class Solution {
public:
    bool isPalindrome(int x) {
        // 特殊情况：
        // 如上所述，当 x < 0 时，x 不是回文数。
        // 同样地，如果数字的最后一位是 0，为了使该数字为回文，
        // 则其第一位数字也应该是 0
        // 只有 0 满足这一属性
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }

        int revertedNumber = 0;
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }

        // 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数字。
        // 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，
        // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。
        return x == revertedNumber || x == revertedNumber / 10;
    }
};

public class Solution {
    public bool IsPalindrome(int x) {
        // 特殊情况：
        // 如上所述，当 x < 0 时，x 不是回文数。
        // 同样地，如果数字的最后一位是 0，为了使该数字为回文，
        // 则其第一位数字也应该是 0
        // 只有 0 满足这一属性
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }

        int revertedNumber = 0;
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }

        // 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数字。
        // 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，
        // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。
        return x == revertedNumber || x == revertedNumber / 10;
    }
}

class Solution {
    public boolean isPalindrome(int x) {
        // 特殊情况：
        // 如上所述，当 x < 0 时，x 不是回文数。
        // 同样地，如果数字的最后一位是 0，为了使该数字为回文，
        // 则其第一位数字也应该是 0
        // 只有 0 满足这一属性
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }

        int revertedNumber = 0;
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }

        // 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数字。
        // 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，
        // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。
        return x == revertedNumber || x == revertedNumber / 10;
    }
}

var isPalindrome = function(x: number): boolean {
    // 特殊情况：
    // 如上所述，当 x < 0 时，x 不是回文数。
    // 同样地，如果数字的最后一位是 0，为了使该数字为回文，
    // 则其第一位数字也应该是 0
    // 只有 0 满足这一属性
    if (x < 0 || (x % 10 === 0 && x !== 0)) {
        return false;
    }

    let revertedNumber: number = 0;
    while (x > revertedNumber) {
        revertedNumber = revertedNumber * 10 + x % 10;
        x = Math.floor(x / 10);
    }

    // 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数字。
    // 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，
    // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。
    return x === revertedNumber || x === Math.floor(revertedNumber / 10);
};

func isPalindrome(x int) bool {
    // 特殊情况：
    // 如上所述，当 x < 0 时，x 不是回文数。
    // 同样地，如果数字的最后一位是 0，为了使该数字为回文，
    // 则其第一位数字也应该是 0
    // 只有 0 满足这一属性
    if x < 0 || (x % 10 == 0 && x != 0) {
        return false
    }

    revertedNumber := 0
    for x > revertedNumber {
        revertedNumber = revertedNumber * 10 + x % 10
        x /= 10
    }

    // 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数字。
    // 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，
    // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。
    return x == revertedNumber || x == revertedNumber / 10
}

复杂度分析

• 时间复杂度：O(log⁡n)O(\log n)，对于每次迭代，我们会将输入除以 1010，因此时间复杂度为 O(log⁡n)O(\log n)。
• 空间复杂度：O(1)O(1)。我们只需要常数空间存放若干变量。

买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

我们需要找出给定数组中两个数字之间的最大差值（即，最大利润）。此外，第二个数字（卖出价格）必须大于第一个数字（买入价格）。

C++代码实现如下↓↓↓

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (!prices.size())
            return 0;
        
        int maxVal = 0;
        int Fiminus1 = 0, Fi = 0;
        for (int i = 1; i <  prices.size(); i++) {
            Fi = max(Fiminus1 + prices[i] - prices[i-1],  0);
            maxVal = max(Fi, maxVal);
            Fiminus1 = Fi;
        }
        return maxVal;
    }   
};

罗马数字转整数

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如， 罗马数字 2 写做 II ，即为两个并列的 1 。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
给定一个罗马数字，将其转换成整数。

示例 1:

输入: s = “III”
输出: 3
示例 2:

输入: s = “IV”
输出: 4
示例 3:

输入: s = “IX”
输出: 9
示例 4:

输入: s = “LVIII”
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:

输入: s = “MCMXCIV”
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

int romanToInt(char * s){
 int i;
    int n;
    int sum=0;
    int len=strlen(s);
    int a[15]={0};

    for(i=0;i<len;i++){
        switch(s[i]){
            case 'M':
                a[i]=1000;
                break;
            case 'D':
                a[i]=500;
                break;
            case 'C':
                a[i]=100;
                break;
            case 'L':
                a[i]=50;
                break;
            case 'X':
                a[i]=10;
                break;
            case 'V':
                a[i]=5;
                break;
            case 'I':
                a[i]=1;
                break;
        }
    }
    if(len==1) return sum=a[0];

    for(n=0;n<len-1;n++){
        if(a[n]<a[n+1]){
            sum=sum+(a[n+1]-a[n]);
            n++;
        }
        else{
            sum=sum+a[n];
        }
        if(n==len-2) sum=sum+a[len-1];
    }

    return sum;
}

最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 “”。

示例 1：

输入：strs = [“flower”,“flow”,“flight”]
输出：“fl”
示例 2：

输入：strs = [“dog”,“racecar”,“car”]
输出：“”
解释：输入不存在公共前缀。

char * longestCommonPrefix(char ** strs, int strsSize){
    int i=0;
    int j=0;
    char tmp=strs[j][i];
    for(i=0;1;i++){
        tmp=strs[0][i];
        for(j=0;j<strsSize;j++){
            if(strs[j][i]=='\0'){
                return strs[j];
            }
            if(tmp!=strs[j][i]){
                if(i==0){
                    strs[0][i] = '\0';
                    return *strs;
                } else {
                    strs[0][i] = '\0';
                    return *strs;
                }
            }
        }
    }
    return *strs;
}

输油管道问题

1.输油管道问题(只考虑y)

某石油公司计划建造一条由东向西的主输油管道。该管道要穿过一个有n 口油井的油田。从每口油井

都要有一条输油管道沿最短路径(或南或北)与主管道相连。如果给定n口油井的位置，即它们的x 坐标（东

西向）和y 坐标（南北向），应如何确定主管道的最优位置，即使各油井到主管道之间的输油管道长度总

和最小的位置？证明可在规定时间内确定主管道的最优位置。

【编程任务】

给定n 口油井的位置,编程计算各油井到主管道之间的输油管道最小长度总和。

输入描述:

第1 行是油井数n，1≤n≤10000。接下来n 行是油井的位置，每行2个整数x和y，-10000≤x,y≤10000。

输出描述:

第1 行中的数是油井到主管道之间的输油管道最小长度总和。

示例1

输入

5

1 2

2 2

1 3

3 -2

3 3

输出

6

代码：

#include<bits/stdc++.h>

using namespace std;

#define ll long long int

bool cmp(int x,int y)

{

return x<y;

}

ll a[200020]={0},b[200020];

int main()

{

int n,i,j,k;

cin>>n;

for(i=0;i<n;i++)

{

​ cin>>a[i]>>b[i];

}

//这个题只需要看y就行了，不需要去关注x的情况。

​ //对b进行排序，只要找到中间的数即可

​ //也就是说找到对于b的取值最大最小之间的数，然后看b到这个数的值，找出来这个最小值

​ //也就是计算到b[n/2]的距离

sort(b,b+n,cmp);//sort排序

int sum=0;

for(i=0;i<n;i++)

{

​ sum+=fabs(b[i]-b[n/2]);

}

cout<<sum;

return 0;

}

2.士兵站队问题(x和y都要考虑)

在一个划分成网格的操场上，n个士兵散乱地站在网格点上。网格点由整数坐标(x,y)表示。士兵们可

以沿网格边上、下、左、右移动一步，但在同一时刻任一网格点上只能有一名士兵。按照军官的命令，士

兵们要整齐地列成一个水平队列，即排列成(x,y),(x+1,y),…,(x+n-1,y)。如何选择x 和y的值才能使士兵们以最少的总移动步数排成一列。

【编程任务】

计算使所有士兵排成一行需要的最少移动步数。

输入描述:

计算使所有士兵排成一行需要的最少移动步数。

输出描述:

第1 行是士兵数n，1≤n≤10000。接下来n 行是士兵的初始位置，每行2 个整数x 和y，-10000≤x，

y≤10000。

示例1

输入

5

1 2

2 2

1 3

3 -2

3 3

输出

8

代码：

#include<bits/stdc++.h>

using namespace std;

#define ll long long int

bool cmp(int x,int y)

{

return x<y;

}

ll a[200020]={0},b[200020];

//这个题就需要对x进行存储，进行计算了

//对于y来说还是和之前一样的操作

//对于x来说需要改变一下

//假设第一个数排在k+1处，后面的依次类推

//那么需要进行的变化就是(a[0]-(k+1)) (a[1]-(k+2)) …

//那么对它进行变化— —变成((a[0]-1)-k) …

//那么对于每一个a[i]都是先减去了一个i+1，再减去了一个k

//这个时候可以想到对y进行的操作不就是共同减去了一个y轴上的数值的中位数吗

//所以先对x进行一次排序，然后减去一个i+1

//再次排序，和y进行相同的操作

int main()

{

int n,i,j,k;

cin>>n;

for(i=0;i<n;i++)

{

​ cin>>a[i]>>b[i];

}

sort(a,a+n,cmp);

sort(b,b+n,cmp);

for(i=0;i<n;i++)

{

​ a[i]=a[i]-i;

}

sort(a,a+n,cmp);

int sum=0;

for(i=0;i<n;i++)

{

​ sum+=fabs(a[i]-a[n/2]);

​ sum+=fabs(b[i]-b[n/2]);

​ //cout<<sum<<endl;

}

cout<<sum;

return 0;