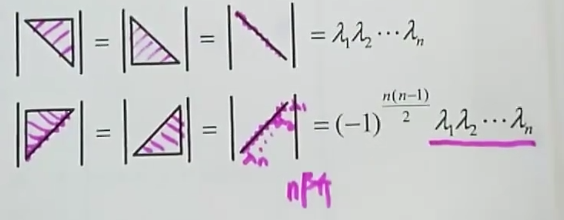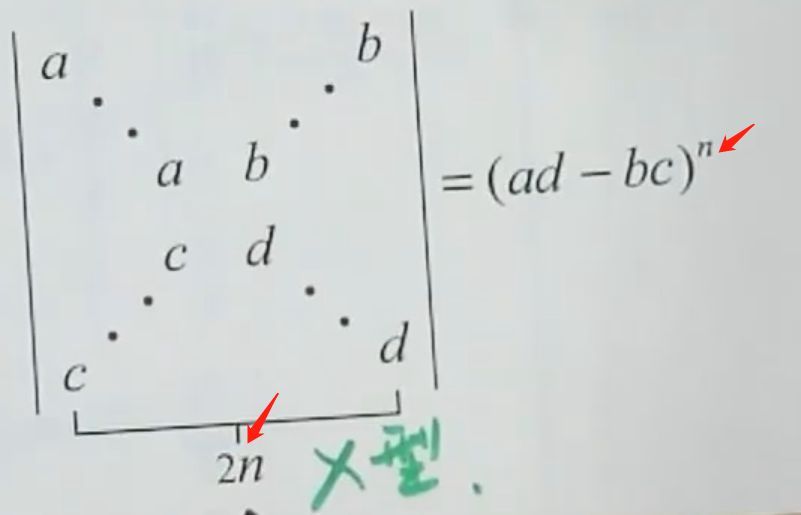线性代数
摘要:
线性代数
常见行列式
箭型行列式
一般的箭型行列式形式如下:(元素间用逗号分隔,行与行之间用分号分隔,下同)
|x, b1, …, bn;a1, d1, …, 0; …, …, …, …;an, 0, …, dn|.
接下来,给出思路和推算的过程。我们可以把箭型行列式转化成上三角行列式。而上三角行列式等于主对角线上所有元素的积。转化过程都是运用行列式的初等变换。
将第二列乘以-a1/d1,第三列乘以-a2/d2,……,第n+1列乘以-an/dn,全部加到第一列,行列式就变成如下形式:
|x-∑(i=1->n)(aibi)/di, b1, …, bn;0, d1, …, 0; …, …, …, …;0, 0, …, dn|.
这是一个上三角行列式,结果就等于主对角线上所有元素的积,从而得到最后的结果。
D=|x, b1, …, bn;a1, d1, …, 0; …, …, …, …;an, 0, …, dn|=(x-∑(i=1->n)(aibi)/di)∏(i=1->n)di.
下面举一个实例,并应用上面推出的公式来解这个行列式,如下:
求行列式D=|2,1,4,3;3,4,0,0;-1,0,-3,0;-2,0,0,-4|.
代入箭型行列式的公式,很容易就可以求得,这个行列式D=(2-(3/4+4/3+3/2))X4X(-3)X(-4)=D=-96.
再举一个例子:求行列式D=|2,1,1/2,…,1/n; 1,4,0,…,0; 2,0,6,…,0;…, …, …, …, …; n, 0, 0, …, 2n+2|。
同样运用箭型行列式的公式,可求得D=(2-∑(i=1->n)(1/(2n+2))∏(i=1->n)(2n+2).
另外箭型行列式还可以变形成同三角行列式(又称为同旁行列式)和同三角同对角元行列式(又称为同旁同角行列式),它们的格式分别如下:
同旁行列式
|b1, a, …, a;a, b2,…,a; …, …, …,…; a, a, a, bn|;
同旁行列式转换为箭型行列式的方法是:在行列式前面增加一行一列,增加的行是1,a, a, …, a; 而除了第一个元素之外,第一列全是0,这样行列式的值就不变;然后从第二行开始,每行都减去第一行。
同旁同角行列式(和相同)
|b, a, …, a;a, b,…,a; …, …, …,…; a, a, a, b|。
同旁同角行列式是同旁行列式的特例,直接运用同旁行列式的公式就可以了。
三对角行列式
数学技巧篇47:三个对角线行列式算法与证法 - 知乎 (zhihu.com)
范德蒙德行列式与爪型行列式
【线性代数(6)】范德蒙德行列式及克莱姆法则_行列式展开公式有多少次乘法克莱姆_lys_828的博客-CSDN博客
线性代数(2):特殊行列式_爪哇-毛毛虫的博客-CSDN博客
简单总结(必看)
考点一、范德蒙行列式
要求
- 第一行/列都是1,结果完全取决于第二行
考点二、上/下三角形行列式
题项1
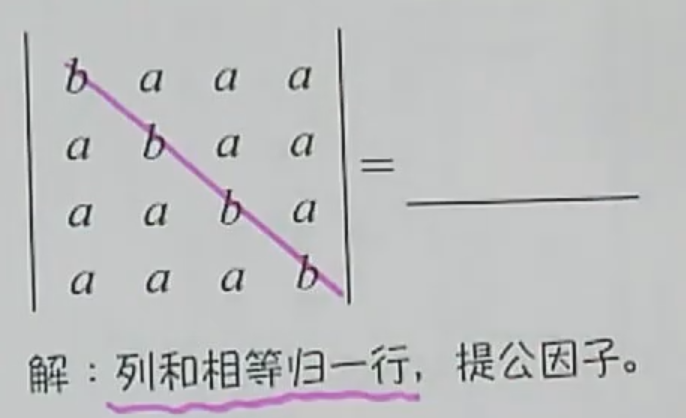
类型:每行/列相加的值相等
方法:将每一行加到同一行,然后提取公因子
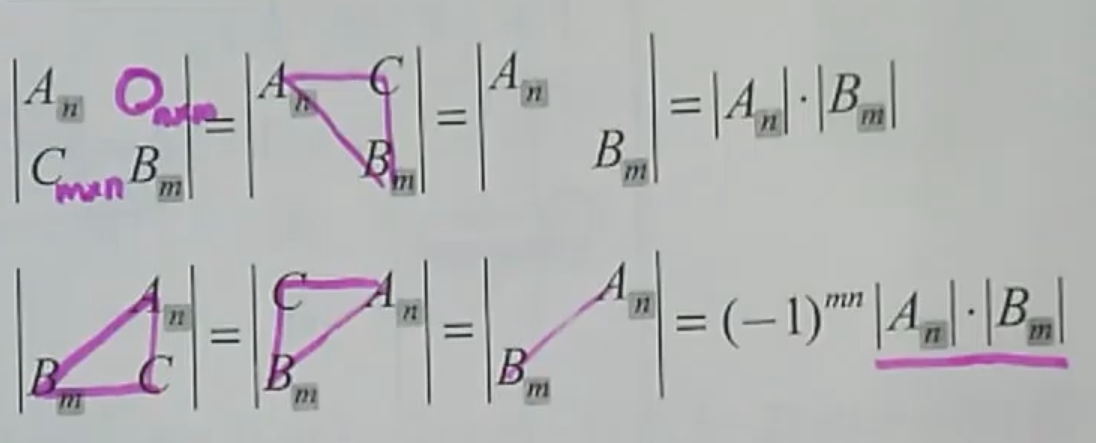
考点三、分块三角形行列式
类型:
公式:
【003 分块行列式计算解析】https://www.bilibili.com/video/BV1dg4y1b7Qp?vd_source=626e2d95a6f6efebc61310d99bac2d29
考点四、两线一星型行列式
类型:
考点五、X形行列式
类型:
方法:
考点六、箭头形行列式
类型:
思路:
如果一行里面只有两个元素,尽可能的让他们成为相反数,然后加到一行出现全是0的列
考点七、加边法
类型:
除了主对角线上的元素都是相等的
加边成为箭头形行列式